Problem - Leetcode
Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.
Example 1:

Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where the width of each bar is 1. The largest rectangle is shown in the red area, which has an area of 10 units.
Example 2:
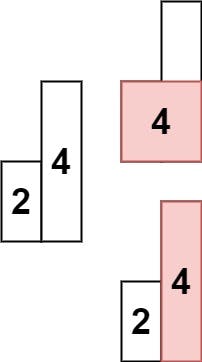
Input: heights = [2,4]
Output: 4
Solution in Golang
func largestRectangleArea(heights []int) int {
stack := []StackValue{}
maxArea := 0
var start int
for i,h := range heights {
start = i
for len(stack) != 0 && stack[len(stack)-1].height > h {
index, height := stack[len(stack)-1].index , stack[len(stack)-1].height
stack = stack[0:len(stack)-1]
maxArea = max(maxArea, height*(i-index))
start = index
}
stack = append(stack, StackValue{start,h})
}
for _, h := range stack {
maxArea = max(maxArea, h.height*(len(heights)-h.index))
}
return maxArea
}
type StackValue struct {
index int
height int
}
func max(a,b int) int {
if a > b {
return a
}
return b
}
This Go code defines a function largestRectangleArea that calculates the largest area of a rectangle that can be formed within a given histogram represented by an array of integer heights. The code uses a stack data structure to efficiently compute this.
Here's a step-by-step explanation of the code:
stack := []StackValue{}: Initialize an empty stack to keep track of heights and their corresponding indices in the histogram.maxArea := 0: Initialize a variablemaxAreato store the maximum rectangle area found so far.var start int: Initialize a variablestartto keep track of the starting index of a potential rectangle.Loop through the input
heightsarray using a for loop withirepresenting the current index andhrepresenting the current height.Set
startto the current indexi.Check if the stack is not empty and the height at the top of the stack (
stack[len(stack)-1].height) is greater than the current heighth. If this condition is true, it means we can potentially calculate the area of a rectangle.Inside the loop, pop elements from the stack while the condition in step 6 is met. For each popped element, calculate the area it represents (height times the width, which is the difference between the current index
iand the index stored in the popped element). UpdatemaxAreaif this area is greater than the currentmaxArea.Set
startto the index of the last popped element, as this is the starting index of the potential rectangle that includes the current heighth.Push the current index
startand heighthonto the stack as aStackValue.After the loop, there might still be elements left in the stack. Loop through these remaining elements and calculate the area for each of them, considering the entire remaining width of the histogram. Update
maxAreaif any of these areas is greater than the currentmaxArea.Finally, return the
maxArea, which represents the largest rectangle that can be formed within the given histogram.
The StackValue struct is used to store the index and height of elements pushed onto the stack.
The max function is a simple utility function used to find the maximum of two integers.
This code essentially uses a stack to keep track of ascending heights in the histogram and calculates the maximum rectangle area that can be formed efficiently.

